RUMUS TRIGONOMETRI
Sumber : https://rumushitung.com/2014/04/29/rumus-rumus-trigonometri-plus-trik/
Silahkan dibaca dengan seksama ya teman-teman
Apa itu Trigonometri
Kalau sobat ditanya apa itu trigonometri kira-kira mau menjawab apa hayooo. Sobat, ternyata trigonometri berasal dari bahasa yunani “trigonon” yang bermakna segitiga dan “metron” yang berarti pengukuran. Trigonometri muncul di awal abad ke-3 masehi. Ia adalah salah satu cabang dari ilmu hitung (matematika) yang mempelajari segitiga meliputi semua aturan dalam penghitungan yang melibatkan sisi dan sudut dalam segitiga.
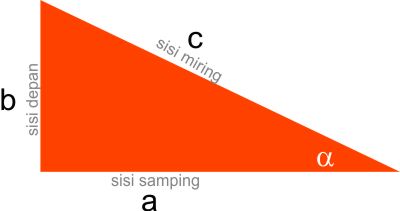
Trigonometri terdiri dari sinus (sin), cosinus (cos), tangen (tan), cotangen (cot), secan (sec), dan cosecan (cosec). Untuk lebih memahami definisi trigonometri yuk simak gambar segitiga di bawah ini.
| Rumus Trigonometri | Keterangan |  |
| Sin α = b/c | sisi depan dibagi sisi miring | |
| Cos α = a/c | sisi samping dibagi sisi miring | |
| Tan α = b/a | sisi depan dibagi sisi samping | |
| Cot α = a/b | sisi samping dibagi sisi depan (kebalikan dari tangen) | |
| Sec α = c/a | sisi miring dibagi sisi samping (kebalikan dari cos) | |
| Cosec α = c/b | sisi miring dibagi sisi depan (kebalikan dari sin) |
Nilai Trigonometri Sudut-Sudut Istimewa
Dalam trigonometri ada lima (kaya poweranger) sudut yang disebut sebagai sudut istimewa yaitu 0o, 30o, 45o, 60o, dan 60o. Penting bagi kita untuk mengetahui besarnya nilai trigonometri sudut-sudut tersebut karena rajin sekali muncul dalam soal ulangan atau ujian nasional. Rangkuman lengkap tentang nilai trigonometri dari sudut tersebut bisa di baca di tabel trigonometri sudut istimewa.
Rumus-Rumus Identitas Trigonometri
Nah ada istilah baru lagi ni, “identitas trigonometri”. Apa coba itu? Identitas trigonometri adalah sifat unik yang hanya dimiliki oleh trigonometri seperti sifat anomali pada air. Sifat itu hanya miliknya. Kalau dikelompokkan, sifat identitas ini bisa di bagi menjadi 3 kelas. Kelas yang pertama adalah identitas pebandingan, kelas kedua identitas kebalikan, dan yang terakhir identitas phytagoras. Berikur rumus trigonometri tersebut
| Identitas Perbandingan | Indentitas Kebalikan | Indentitas Phytagoras |
 |
 |
 |
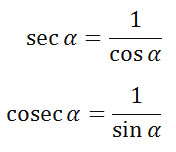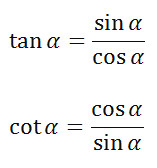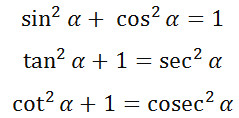Relasi Sudut dalam Trigonometri
Dalam trigonometri, ada relasi atar sudut-sudut. Sudut-sudut di kuadran II (90o-180o), kuadran III (180o-270o) dan kuadran IV (270o-360o) punya relasi dengan sudut-sudut di kuadran I (0o-90o). Berikut rumus-rumus sudut berelasi dalam trigonometri berikut trik untuk menghapalnya.
| 1. (180o – α) –> Kuadran IIsin (180o – α) = sin α
cos (180o – α) = -cosα tan (180o – α) = sin α |
6. (90o – α) –> Kuadran Isin (90o – α) = cos α
cos (90o – α) = sin α tan (90o – α) = cot α |
| 2. (180o + α) –> Kuadran IIIsin (180o + α) = -sin α
cos (180o + α) = -cosα tan (180o + α) = sin α |
7. (90o + α) –> Kuadran IIsin (90o + α) = cos α
cos (90o + α) = -sin α tan (90o + α) = -cot α |
| 3. (360o – α) –> Kuadran IVsin (360o – α) = -sin α
cos (360o – α) = cosα tan (360o – α) = -sin α |
8. (270o – α) –> Kuadran IIIsin (270o – α) = -cos α
cos (270o – α) = -sin α tan (270o – α) = cot α |
| 4. (360o + α) –> Kuadran Isin (360o + α) = sin α
cos (360o + α) = cosα tan (360o + α) = sin α |
9. (270o + α) –> Kuadran IVsin (270o + α) = -cos α
cos (270o + α) = sin α tan (270o + α) = -cot α |
| 5. untuk sudut (-α) –> Kuadran IVsin (-α) = -sin α
cos (-α) = cosα tan (-α) = -sin α |
|
| Rumus Cepat | Rumus Cepat |
| Pola (lihat di kanan tanda =)Sin → Sin Cos → Cos Tan → Tan |
Pola (lihat di kanan tanda =)Sin → Cos Cos → Sin Tan → Cot |
|
Penentuan +/- dilihat dari Kuadran, aturannya
yang POSITIFKuadran I = All (semua)Kuadran II = hanya SINKuadran III = hanya TAN
Kuadran IV = hanya COS sobat bisa mengingatnya ALL SIN TAN COS |
|
Jadi yang perlu sobat lakukan adalah menghafal pola dari sudut istimewa yang kelipatan 180o dan 90o kemudian tentukan hasilnya apakah positif atau negatif dengan menggunkan aturan ALL SIN TAN COS. Contoh soalnya seperti berikut
Sobat ditanya berapa nilai sin 120o? sobat dapat menggunakan trik rumus trigonometri di atas.
Cara I
ingat, 120 = 90 + 30, jadi sin 120o dapat dihitung dengan
Sin 120o = Sin (90o + 30o) = Cos 30o (nilainya positif karena soalnya adalah sin 120o, di kuadran 2, maka hasilnya positif)
Cos 30o = ½ √3
Cara II
sobat bisa juga menggunakan rumus lain untuk soal trigonometri tersebut, 120o nilanya juga sama seperti 180o-80o.
Sin 120o = Sin (180o – 60o) = sin 60o = ½ √3
Terima kasih artikel trigonometrinya. bermanfaat bagi saya.